Introduction
The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.
— Satoshi Nakamoto, Bitcoin: A Peer-to-Peer Electronic Cash System
In the Bitcoin system, miners timestamp blocks of digital transactions, allowing users of the network to send and receive funds while avoiding the double spend problem. Bitcoin and Ethereum use proof-of-work to form consensus around chains of timestamped blocks without reliance on a trusted central authority. Tezos does the same, although with a proof-of-stake consensus mechanism instead.
In all three systems, users may include arbitrary memo’s in transactions. This allows users to timestamp not only transactions but entire documents, by including the documents in the transaction’s memo. The use of Bitcoin in this way has historically been controversial, but smart contract platforms like Tezos are designed for it.
Such a timestamping mechanism has a wide variety of uses, including certifying documents such as laws or end-user-agreements, granting resource rights like domain names, and authenticating predictions of future events. However, blockchain computation and storage are expensive, as the each transaction and bit of data stored are replicated across many nodes. If every application had to pay a transaction fee for each piece of information they timestamped, the costs would prove infeasible for all but a handful of niche domains. Thankfully, with some clever restructuring of the data, we can make a single hash go much further. We introduce a protocol and service for this on the Tezos blockchain called TzStamp.
Previous Work
TzStamp is closest to the design of OpenTimestamps. The first solutions to extend blockchain timestamping took a public list of hashes from users and uploaded the hash of the list. This had the downside of forcing anyone who wanted to verify a timestamp to have access to the entire list. As the lists grew longer this became de-facto centralization. OpenTimestamps avoids this by using a Merkle tree structure to store its hashes. A Merkle tree works by starting with a base layer of items called “leaves”. A tree is then constructed by dividing the leaves into pairs and hashing them, halving the number of items. This process is repeated until there is a single hash left called the Merkle root. The advantage of the Merkle tree is that it reduces the number of hashes required to verify an item is a member of the tree to the logarithm of the number of leaves. This means each item can have the proof of its timestamp reduced to kilobytes even for very large sets of leaves. Therefore it becomes trivial for an end user to store the information necessary to prove their timestamp.
The TzStamp Process
The TzStamp process consists of three events:
- A user submits data to be stamped and receives the “unresolved proof”.
- The TzStamp server publishes the operation on-chain the background and constructs the “affixed proof” using data from a connected Tezos node.
- A user later verifies the data with the proof has a valid timestamp, proving its existence at that time on-chain.
Submitting Data to TzStamp
A user can submit a file to be stamped by the TzStamp server via the website or the CLI. The client hashes the file and sends only the hash. The server then aggregates these hashes into an internal Merkle tree called the “aggregator”. The server returns to the user the minimum list of tree nodes required to reconstruct the Merkle root of the aggregator - this list is called an “unresolved proof” and allows users to prove a particular file hash was included in the aggregator.
On a schedule, the TzStamp server publishes the Merkle root of the aggregator to Tezos inside a transaction to a designated smart contract. Using Tezos indexers, a user can look up the hash aggregator hash that was published in a particular Tezos block and use the unresolved proof to prove a file timestamp was included in that block.
But there’s a catch: Tezos indexer’s periodically purge old transaction data. Anyone can run an archive node themselves and reconstruct the full transaction history; however, this requires days of synchronization and hundreds of gigabytes of data to be downloaded from the network. We thus would like a way to validate timestamps without requiring the full transaction history. Here’s the trick: a Tezos block is identified by its hash, and is itself a kind of Merkle tree that includes the transactions that occurred in the block as leaves in the tree. We’ll outline this schema in the next section. We call the list of data needed to reconstruct this hash the “affixed proof”.
Once a transaction of the aggregator root is included in a block, the TzStamp server uses its connection to a Tezos RPC node to construct the affixed proof. When a user uses the TzStamp server to validate a particular unresolved, the server will send the complete affixed proof in response if it is ready.
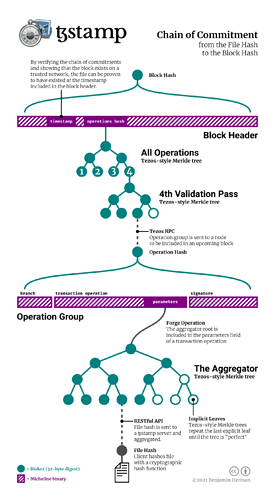
Below is a diagram depicting the protocol:
The proof format is a text file consisting of a series of append, prepend, hash, etc operations. An “operation” is a pure function taking its arguments either from the proof file or the result of the previous operation. Proof documents can be partial, such as the unresolved proof, or they can be be complete, such as the concatenation of the unresolved and affixed proofs returned by the Tzstamp server on verifying a proof successfully included in the chain. A complete proof always includes a final attestation operation which produces a particular block hash on a Tezos network.
In the next sections, we’ll outline the protocol for creating complete proofs. To avoid name clashes, we’ll refer to Tezos network operations as network-operations and TzStamp proof operations as proof-operations.
Constructing The Affixed Proof
At publication time, a network-operation group is locally constructed and signed by the TzStamp server. The aggregator root appears at the parameters.value.bytes field of the transaction-kind operation within the group. The operation is sent to the server’s configured node for inclusion. Once confirmed, the JSON serialization of the full block is fetched.
An operation-less proof is instantiated, taking the aggregator root as input. With no modifying proof-operations, its derivation is the aggregator root. This constitutes the affixed proof.
The process goes as follows:
- The aggregator root is translated to an operation hash.
- The operation hash is aggregated into a an operation(s) hash along with all the other transaction operations in the block.
- The operation(s) hash is aggregated into a block hash, completing the proof.
We’ll go elaborate on each step:
From Aggregator Root To Operation Hash
The Tezos network-operation used to publish the aggregator root is located within the operations lists and extracted. The JSON network-operation is converted into Micheline binary using some custom code. Some fields within the operation group such as its own hash are not part of the binary originally sent to the node for inclusion and are ignored. The operation hash of an network-operation group is the BLAKE2b 32-byte digest of the Micheline binary; so the bytes before and after the aggregator root bytes are embedded in a Join proof-operation, followed by a BLAKE2b proof-operation, which are concatenated to the affixed proof. The derivation of the affixed proof is now the network-operation hash.
From Operation Hash To Operation(s) Hash
The current Tezos network shell uses a four-pass multi-validation schema. Management network-operation groups, including transaction-kind operations, will always appear in the fourth pass. The hash of each pass is the Tezos-style Merkle root containing each operation group in the pass. Tezos-style trees use the BLAKE2b 32-byte digest hash function and implicitly repeat the last leaf until the tree is perfect. If the pass has no operations, the root is the BLAKE2b 32-byte digest of null input.
All network-operation hashes are extracted and built into four Tezos-style Merkle trees, one for each pass. The operation hash of the network-operation used to publish the aggregator root is located within the fourth tree and the join-hash walk from leaf to root is added to the proof. The nodes of the other three pass trees are unneeded. The roots of the pass Merkle trees are then used to build another Tezos-style Merkle tree of size 4. The root of this tree is the operations hash present in the block header. The join-hash walk from the fourth leaf to the root is added to the affixed proof. The derivation of the affixed proof is now the network-operations hash.
From Operation(s) Hash To Block Hash
The block header is extracted and converted into Micheline binary, again ignoring fields such as its own hash that were not present in the original binary. The original header contains both the timestamp and the network-operations hash. The block hash is the BLAKE2b 32-byte digest of the Micheline binary of the header; so the bytes before and after the operations hash are embedded in a Join proof-operation, followed by a BLAKE2b proof-operation, which are concatenated to the affixed proof. The derivation of the affixed proof is now the block hash.
The server tries to verify the affixed proof. If it cannot, a change must have occurred in the protocol and the server will stop taking input.
Constructing The Unresolved Proofs
A proof for each leaf in the aggregator Merkle tree is constructed, their respective inputs being their own bytes and the derivation being the aggregator root. These are the resolved proofs. Each unresolved proof is concatenated with the affixed proof to create a full proof taking the file hash leaf as input and deriving the block hash. The server stores these proofs for later retrieval, and returns them to the user whenever the respective hash’s timestamp is verified.
Credits
Much of the above content was adapted with thanks from the docs written by the original implementors of TzStamp, Benjamin Herman and John David Pressman.