Note : This analysis was done with the help of Arthur Breitman and Bruno Blanchet (Inria). The code used for the analysis can be found at this url.
A new reward formula for Carthage
In this article, we present a new reward formula that we propose for inclusion in Carthage. This new formula is designed to make the network more robust to non-cooperative baking strategies. It does so without changing the total amount of rewards earned by bakers per period of time, i.e. this update should be transparent to bakers and stakers alike.
This work is a follow-up to our previous blog post on Emmy+. It takes into account new criteria to evaluate the performance of non-cooperative baking strategies for the dishonest baker, and a new non-cooperative baking strategy called deflationary baking contributed by a researcher who desires to remain anonymous.
We found this new function more resilient to all non-cooperative baking strategies that we currently know. As a side effect, it slightly increases the variance of rewards. The formula is designed to be less punishing to endorsers whose endorsements are included in blocks of non-zero priority.
The plan of this post is as follows.
- We first give a bit of context explaining how protocol design relies on assumptions on the notions of profitability held by bakers.
- A particular family of noncooperative baking strategies is introduced, corresponding to non-standard notions of profitability. These are the strategies against which we wish to protect the protocol by picking a new reward function.
- We then describe the methodology and rationale that guided us in choosing this new function.
- The results of our analysis confirm the good properties of the new reward function in adversarial settings.
- We conclude this post by listing changes to the RPC API specific to this new function that will be of interest to the Tezos developer community.
Alternative notions of profitability induce different baking strategies
Baking can be framed as a game in which bakers follow strategies aiming at maximizing their profits, for some notion of profitability. A strategy is called cooperative when a baker bakes publicly, on time and includes all available endorsements. Cooperative baking strategies are the ones that provide the chain with the best security, fastest probabilistic finality, and throughput. Nomadic Labs’ baker (which is currently the most widely used) implements such a strategy.
Emmy+ was engineered relying on the assumption that a baker’s notion of profitability is to maximize their reward, so that the dominant strategy for such bakers is cooperative.
However, there are other notions of profitability that we didn’t consider when designing Emmy+ and which induce bakers preferring these notions to deviate from cooperativeness. These other strategies are bad for the protocol (eg they slow down the chain) but are more profitable to bakers pursuing this alternative notion of profitability.
Our new reward function is designed to protect against non-cooperative strategies arising from these new notions of profitability.
In the rest of this post, we will denote Emmy+B and Emmy+C the versions of Emmy+ using respectively the Babylon reward function and the new one we’re proposing for Carthage.
Notions of profitability
Let’s introduce some notations. We will consider the rewards earned by a non-cooperative baker A and those earned by the rest of the delegators aggregated under the name B, over a fixed period of (physical) time. We will denote these respectively r_A, r_B. We will denote their share of the active stake respectively s_A,s_B, with s_A + s_B = 1 (hence we make the choice to ignore undelegated tokens in the inflation computation below). The total supply at the beginning of the time period will be denoted S. For the rest of the article, we take S = 800\times10^6.
When designing the new function, we considered the following notions of profitability:
- Absolute rewards (AR) is the criteria we used in our previous analysis, which corresponds to the total rewards earned per unit of time. This corresponds to maximizing AR = r_A.
- Inflation adjusted rewards (IAR) , also known as the real rate of return . To obtain this function, one considers the rewards relative to the stake, defined as rr_A = \frac{r_A}{S \times s_A}, and correct them by the inflation over the considered period, defined by I =\frac{r_A + r_B}{S}. IAR are defined as relative rewards properly diluted by the inflation, corresponding to the function
- Rewards share difference (RSD) measures the difference in rewards share between the non-cooperative baker and the rest of the network. We define this function as
In other words, a non-cooperative baker wanting to maximize this criterion is willing to lose any token, so long as the others lose more in proportion of their stake.
Non-cooperative baking strategies
As explained in the previous paragraph, bakers have preferences that manifest concretely as notions of profitability. In a second step, these notions, together with contextual information on the preferences of the other bakers, induce baking strategies. In the rest of this post, we will posit a non-cooperative baker acting in a context where the rest of the stake is entirely held by bakers using a cooperative strategy. The strategies we depict are not necessarily optimal in any sense: they must be understood as lower bounds on how toxic non-cooperative strategies can be. These are the strategies we implemented up to now, and against which we aim to protect the protocol.
-
AR block stealing (
ar-attacker) Block stealing is an AR-oriented non-cooperative baking strategy, in which a baker of priority p > 0 will withhold his endorsements in order to slow down the blocks of priority 0,..,p-1 enough for his block to be the fastest one. The decision to perform a steal for an AR-oriented baker will be predicated on checking that the move is both feasible (in terms of delays) and profitable (in the AR sense). Emmy+B was specifically designed to make these steals hard to profit from (see Emmy+ blog post and a recent paper which also analyzes selfish baking in Emmy+B and obtains similar results). -
Deflationary baking + IAR block stealing (
iar-attacker) The IAR-oriented non-cooperative strategy we considered consists in combining block stealing together with deflationary baking . Deflationary baking corresponds to actively refusing to include endorsements of other bakers in one’s blocks. A naive deflationary strategy for baker A is to include his own endorsements plus the minimal amount of endorsements of baker B so that the incurred delay still ensures that his block is faster than the block of baker B with highest priority. An IAR non-cooperative baker will refine this strategy by selecting the IAR-optimal number of endorsements in his deflationary blocks, and also by stealing blocks when feasible (again, optimizing the number of endorsements for the IAR measure). -
Deflationary baking + RSD block stealing (
rsd-attacker) Lastly, we considered an RSD-oriented strategy based on deflationary baking plus RSD-specific block stealing. Similarly to the IAR one, this strategy optimizes the number of endorsements included in all blocks (priority 0 or stolen) according to the RSD criterion.
Methodology of reward function evaluation
Our goal is to determine how non-cooperative strategies deviate from cooperativeness as a function of the stake of a baker following that strategy, assuming the rest of the stake is held by cooperative bakers. Deviation from cooperativeness is measured according to a family of indicators derived from the profitability notions described previously: AR, IAR and RSD.
We independently applied two distinct methodologies to analyze non-cooperative strategies and design our new reward function. This allows us to be fairly confident in the validity of the results we’re about to describe.
- In the first approach, we designed a classical probabilistic model of the baking game to compute (either exactly or numerically) the expected values of the indicators described above, as well as some others. However, we analyzed block stealing and deflationary baking separately. This approach will be presented in detail in a follow-up post.
- The second approach was to implement a generative probabilistic model of the baking game, allowing to simulate the behavior of bakers in various contexts. The programmatic nature of the simulator allows to easily plug in new strategies and new reward functions. The statistics of interest were then obtained by sampling a large number of chains averaging over the empirical distributions obtained this way.
The result of this analysis led us to choose a new reward function, whose design points are the following:
- To make deflationary baking irrational, for all profitability criteria, the reward for including an endorsement is set to the same amount as the reward to have one endorsement included. In other words, the function makes a non-cooperative baker lose as many rewards per censored endorsement as the endorser who loses the endorsement. This property holds only for priority zero. Nevertheless, this is sufficient, because the function is also robust against block stealing, and thus most blocks should be at priority zero. The value is 1.25, or \frac{1}{32}\times 40, giving 40 to the baker and 40 to the endorsers. Note that this will increase the variance of rewards, without impact on the total expected rewards. Concretely, a baker with 100 rolls currently has 57600 ꜩ annual expected reward with an annual standard deviation of 520 ꜩ. With the new reward function, this standard deviation would roughly double at ~1000 ꜩ.
- To make block stealing less profitable, and since the previous point needs to equalize the rewards for the baker and the endorsers of a block, the reward for baking at priority one is set to much less than the reward for baking at priority zero. The value is \frac{6}{32} per included endorsement. The decreasing factor is greater than in Emmy+B, but it is worth the robustness that it gives, as bakes at priority one are bonus tokens anyway.
- On the other hand, the endorsement rewards for endorsements included in priority zero blocks are decreased by a lesser denominator than in Emmy+B (the value is 1.5 instead of 2). This does decrease slightly resistance to block stealing because the baker that steals a block gets a higher reward for his own endorsements, but has the advantage of punishing the endorsers less for having their endorsements not included by absent priority zero bakers.
- All these constants have been chosen to be compatible with the unchanged delay function, as we wanted to keep the extra strong robustness about fork attacks that it brings, as analysed in our blog post on Emmy+.
The final formulas for Emmy+C are as follows. For a block baked at priority p and containing e endorsements, the reward is computed as:
block_reward (p, e) =
if p = 0 then
(e / 32) * 80 * (1/2)
else
(e / 32) * 6
while the reward received for each slot endorsed at priority p is now:
endorsing_reward (p) =
if p = 0 then
(1 / 32) * 80 * (1/2)
else
(1 / 32) * 80 * (1/2) / 1.5
Comparing Emmy+B and Emmy+C
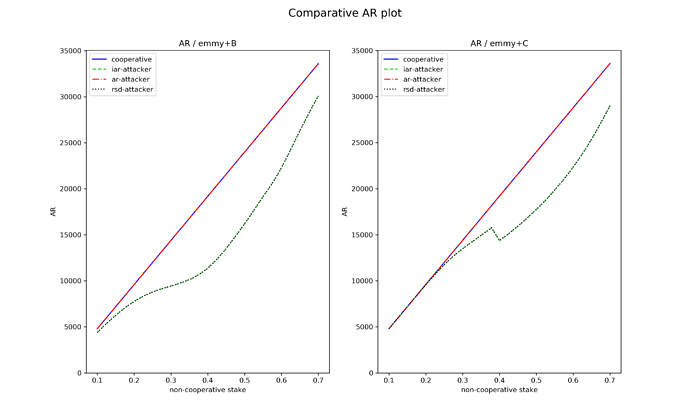
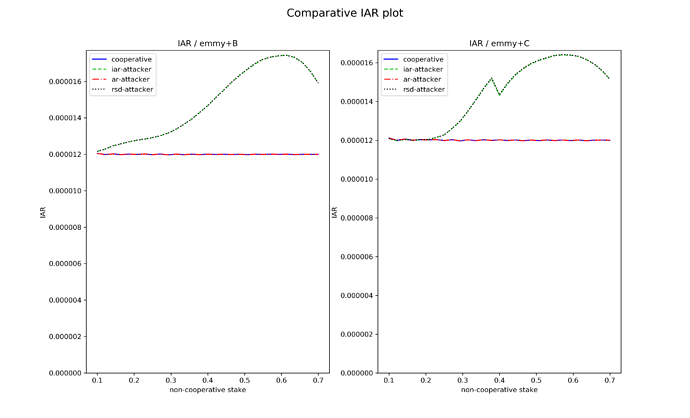
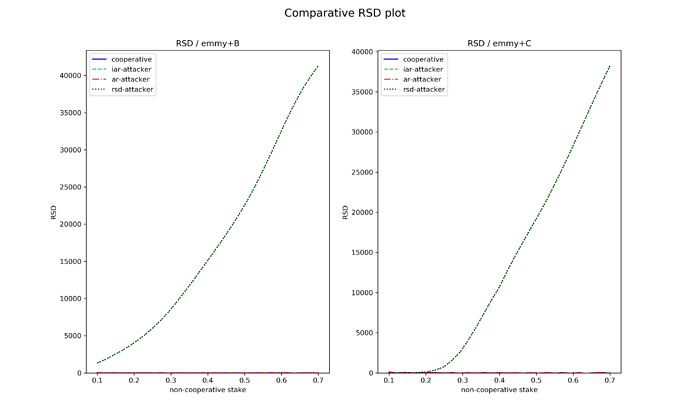
Let us see how this new function fares compared to Emmy+B against the non-conventional baking strategies described above. For each indicator (AR, IAR, RSD) we give two main plots: one for Emmy+B and one for Emmy+C, corresponding to the performance of each baking strategy playing against cooperative bakers, as a function of the stake held by the non-cooperative baker. In addition, we also plot the value of each indicator when the baker plays cooperatively. Each plot corresponds to 8 hours of simulated baking time.
A first observation: the iar-attacker and rsd-attacker perform exactly the same, despite optimizing apparently different criteria.
AR profitability
Let’s start by looking at how these various strategies fare with respect to AR profitability in the case of Emmy+B. The graph below describes the three nonstandard strategies described previously plus a cooperative one. We observe that the cooperative strategy and the ar-attacker strategy clearly dominate the other ones, which is not surprising. What’s more, there seems to be no visible gain by playing the ar-attacker : Emmy+B is well-protected by design against these attacks.
For Emmy+C the picture is similar except for the rsd/iar-attacker strategy which behaves differently (still not getting any noticeable AR gain). The discontinuity in rsd/iar-attacker for Emmy+C is an emergent feature of our strategy and witnesses that it is probably not optimal starting from a non-cooperative stake value of 0.4.
IAR profitability
For Emmy+B, the best IAR strategies are iar-attacker and rsd-attacker which behave identically. Both have a nonnegligible effect starting at very low attacker stake, which is clearly not a good thing. The effectiveness of both strategies peaks at around 60\% of stake: after this, the opportunities for block stealing decrease as most blocks belong to the non-cooperative baker.
Emmy+C displays a much better behaviour: the iar/rsd-attacker only becomes noticeably effective starting at roughy 20-25\% of the stake.
RSD profitability
Emmy+B is quite vulnerable to RSD-based attacks as well. iar/rsd-attacker perform similarly for this indicator in the case of Emmy+B and the attack is effective starting at low stakes as well.
On the other hand, Emmy+C makes iar/rsd-attacker ineffective for bakers with less than 20\% of the stake.
These experiments indicate that Emmy+B is not robust against bakers with notions of profitability other than AR, even against only moderatly complex strategies. On the other hand Emmy+C resists against these strategies for non-cooperative bakers holding a share of the stake up to roughly 20-25\%. Above this, Emmy+C still fares comparatively better to Emmy+B. Emmy+C, while theoretically more fragile against AR-based non-cooperative baking strategies, is consistely at least as secure as Emmy+B in our simulations.
Changes to the RPC API
With the new reward formula comes some minor changes to the API. This section presents these modifications.
The structure of the protocol constants was modified to reflect the new formula.
You may access these constants using the RPC /chains/main/blocks/head/context/constants .
TLDR: The constant block_reward was replaced by baking_reward_per_endorsement and the constant endorsement_reward was modified. The rewards constants now contain a per priority reward value that reflects the previously described formulas.
Baking reward per endorsement
The field block_reward is replaced by the field baking_reward_per_endorsement which now contains a list of mutez values.
baking_reward_per_endorsement is the priority-dependent number of tokens awarded to a block producer per endorsement included in his block. The new constants are "baking_reward_per_endorsement": [ "1250000", "187500" ] meaning that a delegate producing a block of priority 0 will be rewarded e \times 1.25 ꜩ with e the number of endorsement included in the block. If a delegate produces a block at priority 1 , then the second value will be used : e \times 0.1875 ꜩ. If the list is smaller than the given priority, the last value will be used. Thus, for the new proposed constants, blocks baked with priorities greater than 0 will receive the same reward: e \times 0.1875 ꜩ.
The new constants were obtained using the reward formula:
- For priority 0, \frac{e}{32} \times 80 \times \frac{1}{2} = e \times 1.25
- For priority 1 and above, \frac{1}{32} \times 6 = e \times 0.1875
Endorsement reward
The field endorsement_reward is also modified into a list of mutez values. The new constant are "endorsement_reward": [ "1250000", "833333" ] . The semantics is similar to baking_reward_per_endorsement : a delegate endorsing a block of priority 0 will be rewarded 1,25 \times e ꜩ with e the number of endorsing slots attributed to the delegate for this level. Moreover, endorsing blocks of priority greater than 0 will be rewarded 0.8333333 \times e ꜩ .
The new constants were obtained using the reward formula:
- For priority 0, \frac{e}{32} \times 80 \times \frac{1}{2} = e \times 1.25
- For priority 1 and above, \frac{e}{32} \times 80 \times \frac{1}{2} \times \frac{1}{1.5} = e \times 0.833333 (rounded to the closest mutez)
Conclusion
Designing a good reward function is a non-trivial task due to the open and continuously evolving nature of the Tezos protocol. However, we have solid tools in our hands to quickly adapt to the unexpected ways in which people interact with the chain. We believe the new reward function is a reasonable compromise between the existing behaviour and increased security against non-standard baking strategies. Therefore it will be part of the next Carthage proposal.